基于属性的加密算法及其应用

发表于 | 更新于 | 评论数： | 阅读次数：
本文字数： 4.6k | 阅读时长 ≈ 4 分钟

基于属性的加密算法及其应用

最近需要做一个属性加密的系统，因此学习一下基于属性的加密算法。

模糊匹配的居于身份（Fuzzy IBE）的加密算法

模糊匹配的基于属性的加密方案由 Amit Sahai和 Brent Waters于 2005年发表 于欧洲密码学会议。在这篇文章中结合实际的解释了属性的概念。并通过给出的方 案进一步的引伸出基于生物属性的模糊匹配的应用场景。

这篇论文基于的场景可以描述如下，首先系统通过一个密钥抽取算法对一个集 合的属性（设为𝜔’）生成对应的公私钥对，之后对明文$M$进行加密。当解密者拥 有的属性私钥集合𝜔满足𝜔和𝜔’的交集的大小大于某个系统设定值$d$，则解密者可以解密获得明文。

简要的协议描述如下：

  • 基本定义：设$G_1$是一个以素数$p$为阶的双线性群，$g$是其生成单元，$e : G_{1} \times G_{1} arrow G_{2}$为一个双线性配对运算。
    $$
    \Delta_{i, s}(X)=\prod_{j \in S, j \neq i} \frac{x-j}{i-j}
    $$
    为拉格朗日参数,$S$是一个在$Z_p$的集合。所有的属性集合为$U$，而所有属性都与$Z_p^*$中的元素关联。

  • 初始设置：对于一个集合的属性，为其随机选择$Z_p$上的$t_i$作为属性的私钥，并且公布属性对应的公钥为
    $$
    {T_{1}=g^{t_{1}}, \cdots, T_{|U|}=g^{t_{|U|} }}
    $$
    而系统的公钥为$Y=e(g, g)^{y}$，系统的管理密钥为$ {t_{1}, \cdots, t_{|U|}}, y$

  • 密钥抽取：对于一组属性集合$\omega \subseteq U$，随机选择一个$d-1$维的多项式$q(x)$使得$q(0)=y$。这样对于用户的私钥$D_{t}, i \in \omega$对应于$T_i$有$D_{i}=g^{\frac{q(i)}{t_{i}}}$。

  • 加密算法：对于集合$\omega^`$和明文$M \in G_{2}$选择随机值$s$，加密后的结果为
    $$
    E=(\omega^{\prime}, E^{\prime}=M Y^{s},{E_{i}=T_{i}^{s}}_{i \in \omega^{\prime}})
    $$

  • 解密算法：对于集合$\omega$如果满足$|\omega \cap \omega^{\prime}| \geq d$则选择任意属于两个集合交集的$d$个元素，利用拉格朗日插值定理，可得
    $$
    E^{\prime} / \sum_{i \in S}(e(D_{i}, E_{i}))^{\Delta_{i, s}(0)}=M
    $$

模糊匹配的基于身份的加密算法为基于属性的加密算法提供了一个雏形，成功 的将刻画身份的ID分解成为了例如性别，年龄，工作单位的集合。并提出，对基 于生物特征，如血型，基因而抽取相应的属性密钥对身份的访问控制和认证的方式 和设想，为基于属性的加密算法的发展奠定了基础。

基于属性的加密方案发展

从模糊匹配的基于身份的加密算法开始，基于属性的密钥引起了越来越多人的 重视，首先由 VGoyal等人于 CCS06[4]的会议上提出了一个有控制结构的基于属性 的加密方案，同时将基于属性的加密算法进行了划分，分为密文政策的属性基加密算法（CPABE）和密钥政策的属性基加密算法（KPABE）,并对这两种基于属性的加密方法进行了比较和分析，并指出作者提出的是一个密钥政策的属性集加密。 之后 Cheung,L等人通过给出固定大小的访问控制表达树在 CCS07上给出了一个基于密文政策的属性基加密方案，同时对于控制结构的表达能力进行了改善。在改善的同时也引入了一些新的问题，比如密钥扩张和可证安全的问题。

V Goyal等人的 Fined-Gained KP-ABE方案

在这篇文章的方案中，作者提出了表达能力更强的控制结构（Access structure）。通过一种树状的结构，可以提供包括与（AND）或(OR)以及门限 （Threshold）的操作。这些操作大大增强了加密系统中对访问控制能力控制的灵 活性。

这篇文章的另一个突出贡献就是提出了对基于属性的加密算法的一种划分，即密文政策和密钥政策。密文政策是指加密系统中，密文对应于一个访问结构而密钥对应一个属性集合，解密者当且仅当拥有的属性集合中的属性能够满足此访问结构才可获得明文。这种设计可以较好的应用与现实的场景，即加密者可以自由的选择对属性的控制，而解密者只经过一次属性密钥分发的过程即可对他被授权解密的信 息进行解密。而密钥政策就是指密钥对应于一个访问结构而密文对应于一个属性集 合，解密者当且仅当拥有的属性集合中的属性能够满足此访问结构时才可解密。这种场景比较适合增加新用户或者新增加用户对特定的静态数据的访问权限。

使用KP-ABE方法我们可以将属性集合和密文存储在一个服务器上，新增用户或新增用户权限的时候，只需针对对应的属性进行分发。

  • 基本定义：

    • 门限（Threshold）：
      一个门限是一个逻辑运算单元，它具有一个阈值$K$和$num$个输入$(𝐾 ≤ 𝑛𝑢𝑚)$，每一个输入只有$ 1/0$两种状态。当状态为$ 1$的输入数 大于等于$ K$时，门限将输出$ 1$，否则则输出$ 0$。对于特殊的门限，例如$K=1$则是对应的或门（OR Gate），当 $K=num$时则是对应于与门(AND Gate)。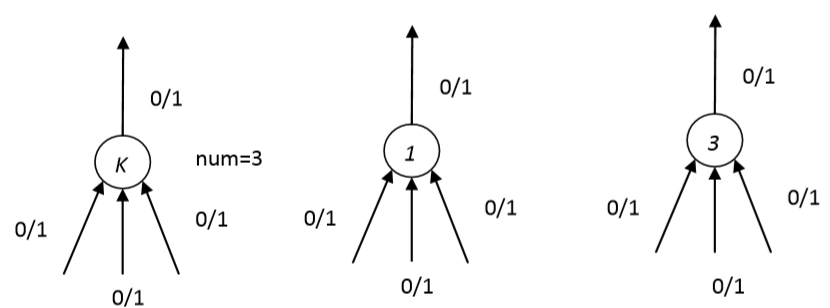

      1557544895950

    • 访问树（Access Tree）：
      访问树用于表达一个控制访问结构。每一个非叶节点都是一个门限，而叶子节点则绑定了某个属性。对于叶子节点$x$，函数$attr(x)$则返回叶子节点相对应的属性。对于任意节点$x$，函数$index(x)$返回该节点对应的索引。如下图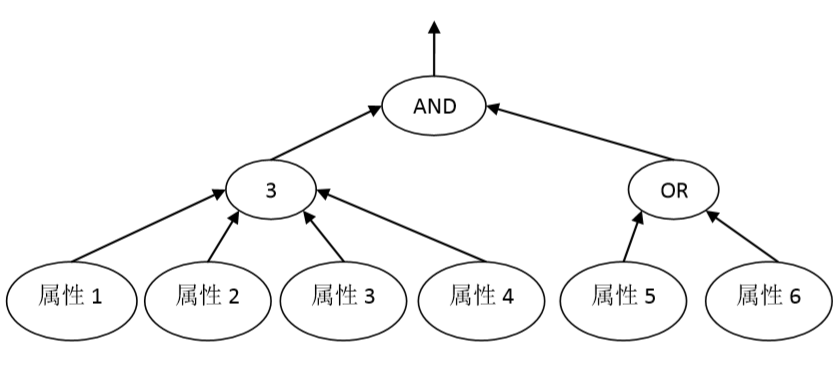

      1557544393172

  • 设$G_1$是一个以素数$p$为阶的双线性群，$g$是其生成元，$e : G_{1} \times G_{1} arrow G_{2}$为一个双线性配对运算。
    $$
    \Delta_{i, s}(X)=\prod_{j \in S, j \neq i} \frac{x-j}{i-j}
    $$
    为拉格朗日参数，$S$是一个在$Z_P$的集合。所有的属性集合为$U$，而所有属性都与$Z_p^*$中的元素相关联。

  • 初始设置：
    对于一个集合的属性，为其随机选择$𝑍_𝑝$上的 ${𝑡_i}$ 作为属性的私钥， 并公布属性对应的公钥为 ${T_{1}=g^{t_{1}}, \cdots, T_{|U|}=g^{t_{|U|} }}$ 。而系统的公钥为$Y=e(g, g)^{y}$，系统的管理密钥为${t_{1}, \cdots, t_{|U|}}, y$。

  • 加密算法：
    对于集合$\omega^{\prime}$和明文$M \in G_{2}$随机选择值，加密后的结果为
    $$
    E=(\omega^{\prime}, E^{\prime}=M Y^{s},{E_{i}=T_{i}^{s}}_{i \epsilon \omega^{\prime}})
    $$

  • 密钥抽取：：对于每一个访问树中的非叶子节点$x$,选择一个多项式$q(x)$,使得它的度为这个节点的阀值减一，即$𝑑𝑥 = 𝑘𝑥 − 1$；对于根节点$ r$则选择$ q_r(0)=y，$而对于其它非叶子结点，使得 $q_x(0)=q_{parent}(index(x))$;针对于叶子结 点的抽取的密钥为
    $$
    K_{x}=g^{\frac{q_{x}(0)}{t_{i}}}, i=\operatorname{att}(x)
    $$

  • 解密算法：对于所有的用户拥有的属性对应的叶子叶结点计算
    $$
    D_{x}=e(k_{x}, E_{i})=e(g, g)^{s \cdot q_{x}(0)}
    $$
    对于非叶子结点利用它的子节点的返回值，由下至上的进行递归运算
    $$
    F_{x}=\sum_{z \in S_{x}} F_{z}^{\Delta_{i}, s_{x}^{\prime}(0)}=e(g, g)^{s \cdot q_{x}(0)}
    $$
    其中 $ i=index(z), S^{\prime}_{x}={index(z) : z \in S_{x}} $。最后可以通过拉格朗日插值定理得到$ e(g, g)^{s y} $，故$ M=E^{\prime} / e(g, g)^{s y} $

Brent Waters的 CPABE方案

在这篇文章的方案中，作者提出了一个标准模型下可证安全的 CPABE 方案， 并且将对控制结构的描述提出了一种新的方式，通过利用线性秘密分享的方案 (LSSS)来决定哪些子集属于授权集合哪些属性的集合不是授权集合。基于这种方案 的属性基的加密打破了原来众多方案只能使用拉格朗日差值定理进行构造的模式， 无论在表述能力上还是安全证明上都有很大的贡献。

  • 基本定义：对于一个属性的集合，如果它满足了对应的控制结构，我们则 称其为一个授权集；对于所有的授权集所组成的集合我们称之为授权集集 合，同时也代表了这一类属性基加密算法的控制结构，我们定义为𝛤。对于线性分享方案 LSSS，对于授权集合中的元素即对应于属性， 每一个矩阵$ M$对应于这些授权集集合𝛤。即对于授权集合中的元素，可以 通过他们的分享恢复出秘密。

  • 初始设置：$G_1$是一个以素数$ p$为阶的双线性群，$g$是其生成元，$e : G_{1} \times G_{1} arrow G_{2}$为一个双线性配对运算。随机地，我们可以在$ Z_p$上选取$ a$和$\alpha$。选择哈希函数$H :{0,1}^{*} arrow G_{1}$

  • 加密算法：对于明文$m$选择随机向量 $v=(s, r_{2}, \ldots, r_{n})$，则$\lambda_i=v*M_i$，密文为$C T=(C=m e(g, g)^{\alpha s}, C^{\prime}=g^{s}, C_{1}=g^{a \lambda_{1}} H(\rho(1))^{-s}, \ldots, C_{l}=g^{a \lambda_{l}} H(\rho(l))^{-s}.$

  • 密钥抽取：对于某一属性的集合$S$，在$Z_p$上随机选取$t$，则密钥为
    $$
    K=(K_{0}=g^{\alpha} g^{a t}, L=g^{t},{K_{x}=H(x)^{t}}_{x \in S})
    $$

  • 解密算法：对于密文$ CT $和线性分享的结构对应的矩阵$(𝑀,\rho)$,满足控制访问 结构的属性集合$ S$对应的密钥$K$，以及线性密钥分享方案对应的常量集合${\omega_𝑖}$，则解密的运算首先计算
    $$
    e(C^{\prime}, K_{0}) /(\Pi_{i \in l}(e(C_{i}, L) e(D_{i}, K_{\rho(i)}))^{\omega_{i}}=e(g, g)^{\alpha s}.
    $$
    之后可以从$C$中分离出明文$m$